Elliptic Curves: Simple Equations Still Shrouded in Mystery

From quadratic equations to the Pythagorean theorem, many areas of arithmetic and geometry are accessible to middle school students, thanks in large part to the mathematicians who discovered them centuries ago.

We often assume that most mysteries of mathematics are largely solved, but that is far from true, says Michele Fornea, a Junior Fellow with the Simons Society of Fellows. As a postdoc at Columbia University under the mentorship of Michael Harris, Fornea is studying a particularly vexing class of polynomial equations that define mathematical objects known as elliptic curves. At first glance, they appear to be simple curves in the xy-plane, but they become more complex upon closer inspection.

Fornea earned his doctorate at McGill University and completed one year as a postdoctoral fellow at Princeton University. He also holds master’s degrees in mathematics from the Université Paris-Sud and Concordia University.

We recently spoke about the elegance and mystery of elliptic curves and the beauty of pure mathematics in general. Our conversation has been condensed and edited for clarity.

First things first: What’s an elliptic curve?

An elliptic curve is a mathematical object that can be described by a deceptively simple equation: y² = x³ + Ax + B. It can resemble a boomerang when plotted on the xy-plane.

As a number theorist, my job is to study the properties of elliptic curves’ rational solutions, that is, the pairs of rational numbers that solve the defining equation once we substitute numbers for x and y. We call these solutions ‘points’ of the elliptic curve.

For example, consider the elliptic curve described by the equation y² = x³ − x + 1. This curve has infinitely many rational points, most of them almost impossible to spot, but we can easily find at least one by setting x = 1 and y = 1.

Why are elliptic curves especially interesting?

One fascinating aspect of elliptic curves is the existence of a ‘geometric’ addition rule on their sets of rational points, one for each specific curve. Essentially, just as we can add whole numbers together, like 7 + 19 = 26, if we are given two points on an elliptic curve, we can obtain a third by ‘summing’ them. The addition rule is best understood by this graphic (see right), though another way to describe it succinctly is by saying that any three points on an elliptic curve ‘sum’ to zero if they belong to the same line.

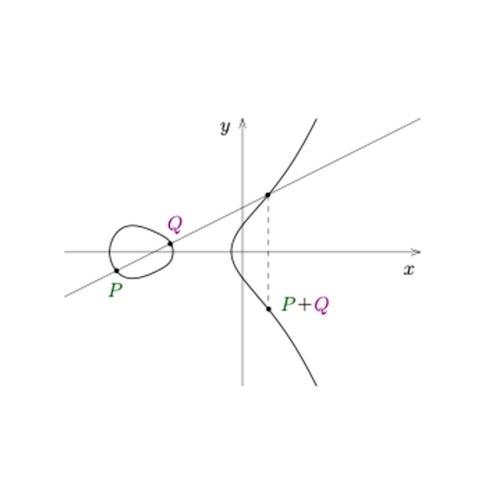
People often wonder why anyone would be interested in studying these equations. One thing about the pure math that I do — called number theory — is that it may or may not lead to practical applications. If practical applications are eventually found, that’s great, but often number theorists simply relish the challenge and process of solving difficult problems, especially those that have an interesting history. My colleagues and I care about understanding the intricacies of polynomial equations like elliptic curves because humankind has been fascinated and frustrated by these problems for thousands of years.

Tell me more about that history.

OK, let’s start from the beginning. We found a way to solve simple equations in one variable a long time ago. As far as we know, ancient Babylonian and Chinese mathematicians were the first to find general solutions to quadratic equations in one variable, as in this equation in which x is the only unknown: ax² + bx + c = 0.

Nowadays, we learn to solve quadratic equations in middle school, but back then it was considered advanced research! It wasn’t until the Middle Ages and, later, the Renaissance that mathematicians identified formulas for more complex equations, cubic and quartic equations, meaning equations in which a variable is raised to the third power (cubic) or fourth power (quartic).

During the Italian Renaissance, believe it or not, mathematicians from different city-states would challenge each other to intellectual duels about how to solve these more complex equations. They also tried hard to find formulas for the general quintic equation (where a variable is raised to the fifth power), but they never succeeded. A few centuries later, we learned why: In the early 1800s, mathematicians Niels Henrik Abel of Norway and Évariste Galois of France showed independently that general solutions to quintic equations (or higher) do not exist.

Fast-forwarding to the present, the simplest family of equations that we don’t fully understand yet is what I study: the family of elliptic curves. Nowadays we are not interested in explicit formulas for points on elliptic curves, but rather in understanding the structural properties that underlie their sets of rational points.

That sounds fascinating! Please elaborate.

To answer, let’s first consider this question: How many rational points does an elliptic curve have? If they always had a finite number, we could simply count them, but often that’s not the case. So, to measure how many points there are — finite and infinite — we use the geometric addition rule that I mentioned earlier. We define the rank of an elliptic curve as the minimal number of points needed to obtain all the other solutions.

For instance, the curve y² = x³ − x + 1 I mentioned before has a rank equal to 1 because it has infinitely many rational points and all of them are multiples of a single point, in this case (1,1). In general, elliptic curves can have rank 0, 1 or higher.

One big open question in the field is the BSD conjecture, which aims to shed light precisely on ranks of elliptic curves. The conjecture was formulated by British mathematicians Bryan John Birch and Peter Swinnerton-Dyer in the late 1960s and remains unproven. Today, the Clay Mathematics Institute is willing to give $1 million to whoever proves it!

Wow! It will be interesting to follow efforts to solve this mystery. What work have you undertaken during your Simons fellowship?

Earlier this year, my collaborators and I released two papers about the arithmetic of elliptic curves. For a long time, number theorists have sought a systematic way to construct meaningful points on elliptic curves of large rank (meaning any rank greater than 1). In our papers we propose one way to do this, and we formulate precise expectations about the relevance of this work for the BSD conjecture.

Of course, our idea didn’t come out of thin air. It was inspired by a pair of powerful insights from various mathematicians in the 2000s: Henri Darmon’s definition of Stark-Heegner points, and Jan Nekovář and Anthony J. Scholl’s plectic conjectures.

I am very pleased with our results because I had been looking to achieve them, in some form or another, since the beginning of my Ph.D. After dozens of ideas that led to nowhere, finally one has a good chance of succeeding!

I hope it does. How has the Simons Foundation helped your work?

The financial support is generous and enables me to pursue research I really care about, and I am very grateful for that.

Because I started my fellowship right as the pandemic began, we haven’t had the benefit of in-person meetings thus far. We’ve had some Zoom dinners and heard some interesting talks from different fellows, but that’s just not the same as gathering in person. But this month we are scheduled for our first in-person meeting, and I’m really looking forward to connecting with the other fellows face to face.