Predicting Neural Dynamics from Neural Connectivity

A new mathematical framework aims to decipher how the structure of a neural network shapes the activity patterns it creates.

The human brain is a dynamic web — 100 billion neurons connected via 100 trillion connections in constant flux. Synapses change as we learn, remember and make decisions, altering the structure of the network and the pattern of activity it produces. These changes modify the brain’s computational repertoire, making us better able to recall a phone number or play a violin.

This process lies at the heart of how the brain works, but neuroscientists know little about the rules that tie neural architecture to function — how different network structures give rise to specific patterns of brain activity, for example. Eric Shea-Brown, a computational neuroscientist at the University of Washington, Seattle, aims to address that question by examining whether a network’s local connectivity can predict its dynamics.

“A trillion different connections could be organized in a galactic number of possible architectures that are impossible to parse,” says Shea-Brown, who presented the research at the Cosyne conference in Portugal in March. “We’d like to build some kind of systematic theory of how specific dynamics arise from connections among neurons; we want to be able to say these are the features of connectivity that matter.”

One way to assess a neural network’s dynamics is through its dimensionality — the number of different features that a neural population encodes. A population that encodes a single feature of an image, such as its brightness, would be one-dimensional, for example. Because all the neurons on the population represent the same feature, their activity can be represented by a single variable.

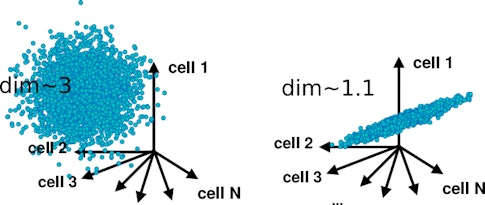
Each axis represents activity of a single neuron. A population of neurons can have low dimensional activity (right), where activity can be roughly represented as a line, or higher dimensional activity (left), where activity fills all three dimensions. Stefano Recanatesi/Shea-Brown lab

In contrast, if every cell encoded the brightness of a different pixel in the image, the population would be high-dimensional, in principle, encoding as many features as there are pixels. In a high-dimensional network, each neuron is largely independent of the others, making it difficult to describe its activity in simpler terms.

Determining a population’s dimensionality is useful because it enables neuroscientists to track how the computational properties of the population change depending on the circumstances. How does learning, which modifies neural connections, alters those dynamics, for example?

In the 1990s, neuroscientists studying neural networks proposed that networks would arrange their connections to maximize the amount of information that they can store, thus generating high-dimensional activity. But as new technologies made it possible to measure dimensionality — namely, through the simultaneous recording of many neurons — researchers made a surprising discovery: neural populations often produce lower-dimensional activity. “Observations of low-dimensionality have been made many times,” says Omri Barak, a theoretical neuroscientist at Technion Israel Institute of Technology. “But little work systematically tries to understand why it arises and give a theory for that.” (Some research suggests that a network’s dimensionality is influenced by the complexity of a task and the number of neurons recorded; see “The Dimension Question: How High Does It Go?”)

Eric Shea-Brown and collaborators want to address this tension by examining how features of the neural network determine its dimensionality. “How can neural connections be organized so that the brain has high-dimensional activity or low-dimensional activity?” he asks. “We hope the answer is short and sweet and local.”

A recipe for neural networks

To date, most efforts to connect network structure and dynamics have focused on networks in which connections are random. “This explains spontaneous activity in the cortex well, but random networks are very limited in explaining how networks compute things,” says Srdjan Ostojic, a neuroscientist at Ecole Normale Supérieure. “We need to go beyond that paradigm, to understand how structure impacts network dynamics. Cortical networks are highly recurrent, they have lots of loops, which can lead to complex dynamics that are hard to understand.”

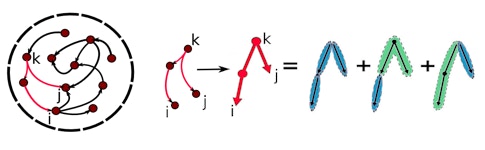
Neural networks can be decomposed into simpler components. The four neuron circuit highlighted in red can be broken down into several motifs, in different ways: three single connections (blue), in which one neuron connects to another; or a combination of a double connection (green), in which one neuron is connected to two others, and one single connection (blue). Credit: Stefano Recanatesi/Shea-Brown lab

To understand how the structure of loops impacts dynamics, Shea-Brown and collaborators start by deconstructing artificial neural networks into simple elements, such as a single connection between two cells. The goal is to create a parts list from which the network builds its various patterns of brain activity. The parts themselves are “not individual neurons but the units in which they self-organize to play out the beautiful activity patterns we see in the brain,” Shea-Brown says.

The key to this decomposition is a formula that predicts longer connectivity patterns, or motifs, based on smaller ones, developed by Yu Hu, formerly a graduate student with Shea-Brown and now at the Hong Kong University of Science and Technology. “You just have to plug in the prevalence of a few short network motifs,” Shea-Brown says, such as the probability that pairs of cells are connected or that three cells are connected in a chain.

“He decomposes the connectivity matrix and looks at how the frequency of each motif contributes to the overall dynamics,” says Brent Doiron, an investigator with the Simons Collaboration on the Global Brain at the University of Pittsburgh. “It’s a powerful idea that can create testable predictions.”

Using this approach, researchers found that characterizing local motifs in spiking network models can predict the majority of dimensionality in excitatory networks. “The parts list of motifs [tells] you most of what you need to know,” Shea-Brown says. “Major trends in the activity dimension can be understood through the lens of local features.”

Both Shea-Brown and others note that the current approach has limitations. So far, it only works in excitatory networks. But researchers are working with theorists in Germany to try to expand it to balanced excitatory-inhibitory networks as well.

Another limitation is that the networks are based on simple mathematical models, sometimes called generalized linear models, that use linear connections among cells. “The theory as we’ve done it so far doesn’t include saturation effects or facilitation effects,” Shea-Brown says. “But even if the mathematical formula doesn’t work because the system is nonlinear, I still believe that local motifs control dimensionality, just in a way that we can’t quantify a priori in a given system.”

The researchers next plan to test the theory experimentally, using local two-photon recordings to calculate functional connectivity and then assessing if these measures predict dimensionality using the Hu equation.

Dialing dimensionality up and down

In addition to analyzing how connectivity governs dynamics, Shea-Brown’s team is exploring how a network’s dimensionality changes as the network learns. “We want to build a theory of what types of learning rules lead to robust changes in dimensionality,” he says.

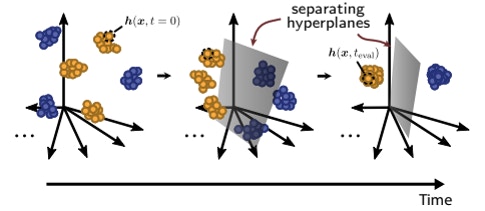
Dimensionality collapses as a trained neural network classifies inputs. At the start of the trial, neural activity is high dimensional (left), reflecting that the network hasn't yet made its choice. As the network processes the inputs, neural activity clusters (blue and yellow) tied to each category become separable (center). When the network arrives at a decision, the clusters are more collapsed than necessary to perform the task, demonstrating a greater than expected collapse in dimensionality. Matthew Farrell/Shea-Brown lab

From a purely behavioral level, one would expect dimensionality to decrease with learning. An animal’s behavior typically becomes more predictable as it learns; a novice tennis player’s serve will vary with each attempt, but a pro looks the same on every swing. This results in a simpler, and thus lower-dimensional, pattern of neural activity.

But does learning diminish dimensionality beyond this expected decline? To address that question, Shea-Brown’s group will examine how the dimensionality of an internal representation of information changes in both animals and artificial neural networks as they learn a classification task. Previous modelling and theoretical work suggests that dimensionality drops when recurrent neural networks learn to classify inputs. However, other studies have found that dimensionality can be dialed up during learning. Shea-Brown’s team plans to test these ideas in collaboration with the Allen Institute.

Shea-Brown points out that shrinking or expanding dimensionality might benefit different types of problems. For example, compressing dimensionality could help with generalization or rapid learning. “Low-dimensional codes are inflexible, because they can work only with the few variables they encode,” Shea-Brown says. “But they are fast. Because they compress huge numbers of inputs together into a low-dimensional set, one example immediately generalizes to any other inputs that have been compressed in the same way.”

Higher-dimensional representations can encode more information and may be better able to create flexible associations. “However, these computations might be complicated to learn, and will require lots of training examples, because each will be represented differently,” Shea-Brown says. “If you want to squeeze as much information as possible out of the brain, you’d expect it to be high-dimensional. But to learn quickly, low-dimensionality is more effective.”